Définition

\(\triangleright\) Définition d'un fluide réel

Un fluide réel est un fluide pour lequel on considère sa Viscosité.
Fluide visqueux

Mise en évidence de la viscosité \(\eta\)

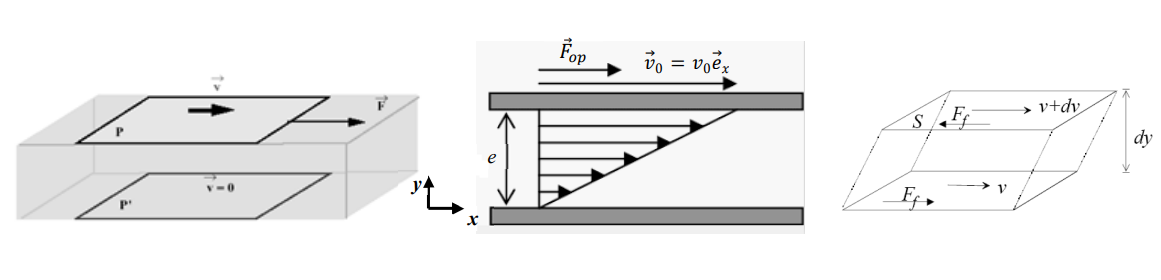
Le mouvement de la plaque supérieur entraine couche par couche le fluide.
En effet, les particules intéragissent de proche en proche, la couche limite intéragit avec la plaque et la couche limite intéragit avec la couche inférieure,...
On parle de Diffusion de la quantité de mouvement.
On traduit ce comportement par la caractéristique dîte de viscosité.

La force exercé sur la plaque entraine sur les couches de fluides une "contrainte de cisaillement" agissant sur la surface. (Contrainte)

Déformations

Les contraintes peuvent engendrer des déformations agissant sur les angles ou sur le volume.

Ces contraintes de cisaillement engendrent un gradient de vitesse latéral, à l’origine de la déformation des particules de fluide. Sur un fluide imcompressible soumis à une contrainte tangentielle, on observe une déformation agissant sur les angles.



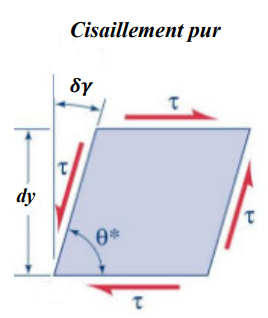
La variation de l'angle est : \(\dot \gamma=\frac{\partial V_x}{\partial y}\)

\(\triangleright\) Force de contrainte de cisaillement

Expérimentalement, on sait que:
$$F_{op}=\eta \frac{Sv_0}{e}$$
Avec:
- \(\eta\): viscosité
- \(S\): surface
- \(v_0\): vitesse
- \(e\): la profondeur du fluide

\(\triangleright\) Contrainte de cisaillement

La contrainte de cisaillement est donné par:
$$\sigma_{xy}={{\eta\dot \gamma}}$$
- \(\eta\): Viscosité
- \(\dot \gamma=\frac{\partial V_x}{\partial y}\): variation de l'angle

Fluide Newtonien

Fluide Newtonien

Fluide non-Newtonien

Fluide non-Newtonien

Nombre de Reynolds: diffusion et convection

On définit le temps de convection \(\tau_{onvection}=\frac{L}{U}\)
Avec:
- \(L\): la longueur de l'écoulement
- \(U\): la vitesse moyenne de l'écoulement

On définit le temps de diffusion \(\tau_{diffusion}=\frac{L^2}{\nu}\)
Avec:
- \(L\): la longueur de l'écoulement
- \(\nu\): Viscosité cinématique
On peut alors comparer ces deux temps caractéristiques pour déterminer le type d'écoulement.
Ce rapport est le Nombre de Reynolds

Force de viscosité

Force de viscosité

Equation de Navier-Stokes

Equation de Navier-Stokes

Perte de charge

Dans un écoulement réel, la pression décroit linéairement dans le sens de l'écoulement.
Cette variation de pression est décrite par la Loi de Poiseuille
On dit qu'il y a perte de charge à cause des forces dissipatives de forttement visqueux entre couches.

Perte de charge linéique